你真的懂递归吗？

因为很多算法思想都基于递归，无论是DFS、树的遍历、分治算法、动态规划等都是递归思想的应用。学会了用递归来解决问题的这种思维方式，再去学习其他的算法思想，无疑是事半功倍的。

递归的本质

无可奈何花落去，似曾相识燕归来。

递归，去的过程叫“递” ，回来的过程叫“归”。

探究递归的本质要从计算机语言的本质说起。

计算机语言的本质是汇编语言，汇编语言的特点就是没有循环嵌套。
我们平时使用高级语言来写的 if..else.. 也好， for/while 也好，在实际的机器指令层面来看，就是一个简单的地址跳转，跳转到特定的指令位置，类似于 goto 语句。

机器嘛，总是没有温度的。我们再来看一个生活中的例子，大家小的时候一定用新华字典查过字。如果要查的字的解释中，也有不认识的字。那就要接着查第二个字，不幸第二个字的解释中，也有不认识的字，就要接着查第三个字。直到有一个字的解释我们完全可以看懂，那么递归就到了尽头。接下来我们开始后退，逐个清楚了之前查过的每一个字，最终，我们明白了我们要查的第一个字。

我们再从一段代码中，体会一下递归。

const factorial = function(n) {
    if (n <= 1) {
        return 1;
    }
    return n * factorial(n - 1);
}

factorial 是一个实现阶乘的函数。我们以阶乘 f(6) 来看下它的递归。

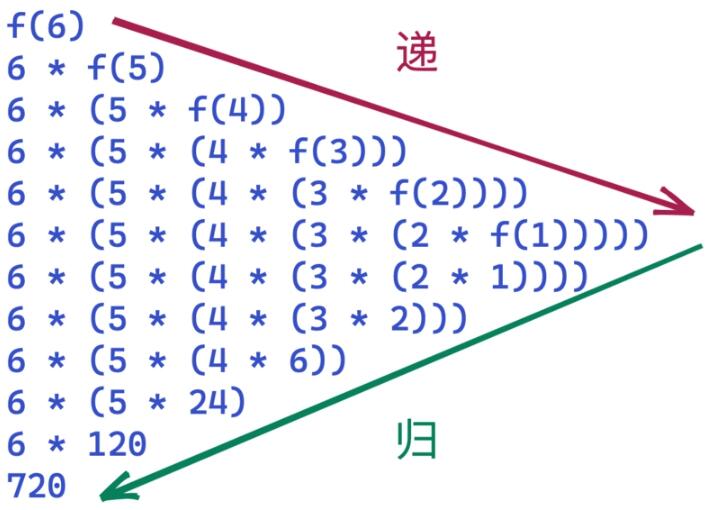
f(6) = n * f(5)，所以 f(6) 需要拆解成 f(5) 子问题进行求解，以此类推 f(5) = n * f(4) ，也需要进一步拆分 ... 直到 f(1)，这是递的过程。 f(1) 解决后，依次可以解决f(2).... f(n)最后也被解决，这是归的过程。

从上面两个例子可以看出，递归无非就是把问题拆解成具有相同解决思路的子问题，直到最后被拆解的子问题不能够拆分，这个过程是“递”。当解决了最小粒度可求解的子问题后，在“归”的过程中顺其自然的解决了最开始的问题。

搞清楚了递归的本质，在利用递归思想解题之前，我们还要记住满足递归的三个条件：

1.问题可以被分解成几个子问题

2.问题和子问题的求解方法完全相同

3.递归终止条件

敲黑板，记笔记！

LeetCode 真题

我们拿一道 LeetCode 真题练练手。

求解斐波那契数列，该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和，也就是：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

给定 N，计算 F(N)。

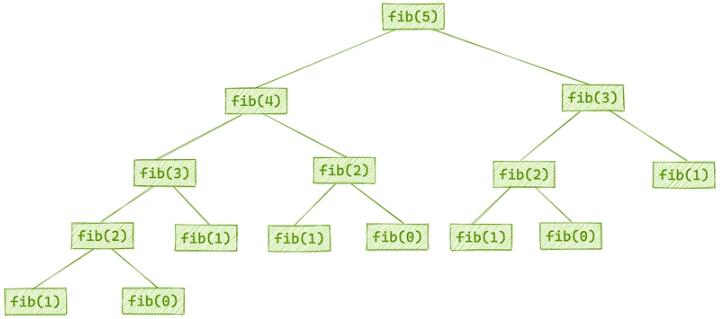
递归树如上图所示，要计算 f(5)，就要先计算子问题 f(4) 和 f(3)，要计算 f(4)，就要先计算出子问题 f(3)和 f(2)...
以此类推，当最后计算到 f(0) 或者 f(1) 的时候，结果已知，然后层层返回结果。

经过如上分析可知，满足递归的三个条件，开始撸代码。

递归解法

const fib = function(n) {
    if (n == 0 || n == 1) {
        return n;
    }
    return fib(n - 1) + fib(n - 2);
}

或者可以这样炫技：

const fib = n => n <= 0 ? 0 : n == 1 ? 1: fib(n - 2) + fib(n - 1);

还没完事，记住要养成习惯，一定要对自己写出的算法进行复杂度分析。这部分在专栏JavaScript算法时间、空间复杂度分析已经讲解过，没看过的同学请点击链接移步。

复杂度分析

空间复杂度为 O(n)
时间复杂度 O(2^n)

总时间 = 子问题个数 * 解决一个子问题需要的时间

子问题个数即递归树中的节点总数 2^n
解决一个子问题需要的时间，因为只有一个加法操作 fib(n-1) + fib(n-2) ，所以解决一个子问题的时间为 O(1)

二者相乘，得出算法的时间复杂度为 O(2^n)，指数级别，裂开了呀。

面试的时候如果只写这样一种解法就 GG 了。

其实这道题我们可以利用动态规划或是黄金分割比通项公式来求解，动态规划想要讲清楚的话篇幅较长，后续开个专栏会详细介绍，这里看不懂的同学们不要着急。

(选择这道题的初衷是为了让大家理解递归。)

动态规划解法

递归是自顶向下(看上文递归树)，动态规划是自底向上，将递归改成迭代。为了减少空间消耗，只存储两个值，这种解法是动态规划的最优解。

时间复杂度 O(n)
空间复杂度 O(1)

const fib = function(n) {
    if (n == 0) {
        return 0;
    }
    let a1 = 0;
    let a2 = 1;
    for (let i = 1; i < n; i++) {
        [a1, a2] = [a2, a1 + a2];
    }
    return a2;
}

黄金分割比通项公式解法

时间复杂度 O(logn)
空间复杂度 O(1)

const fib = function(n) {
    return (Math.pow((1 + Math.sqrt(5))/2, n) - Math.pow((1 - Math.sqrt(5))/2, n)) / Math.sqrt(5);
}

除此之外，还可以利用矩阵方程来解题，这里不再展开。

回到递归，在学习递归的过程中，最大的陷阱就是人肉递归。人脑是很难把整个“递”“归”过程毫无差错的想清楚的。但是计算机恰好擅长做重复的事情，那我们便无须跳入细节，利用数学归纳法的思想，将其抽象成一个递推公式。相信它可以完成这个任务，其他的交给计算机就好了。

如果你非要探究里面的细节，挑战人脑压栈，那么你只可能会陷入其中，甚至怀疑人生。南墙不好撞，该回头就回头。

你凝望深渊的时候，深渊也在凝望你。

原文：https://segmentfault.com/a/1190000022677431

链接: https://fly63.com/article/detial/9061