看了很多文章，梯度下降算法描述都比较艰涩难懂
比如说: 目标函数f(θ)关于参数θ的梯度将是损失函数（loss function）上升最快的方向。然后会推导出下面这个公式。

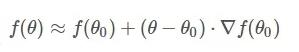
y = x^x求最小值

对于希腊字母本能地觉得很晕，下面将以y = x^x; (0<x<1)求最小值讲解梯度下降算法。

对于y = x^x在0-1中实际上是如下图一个函数，如何求取这个函数的最小值呢？

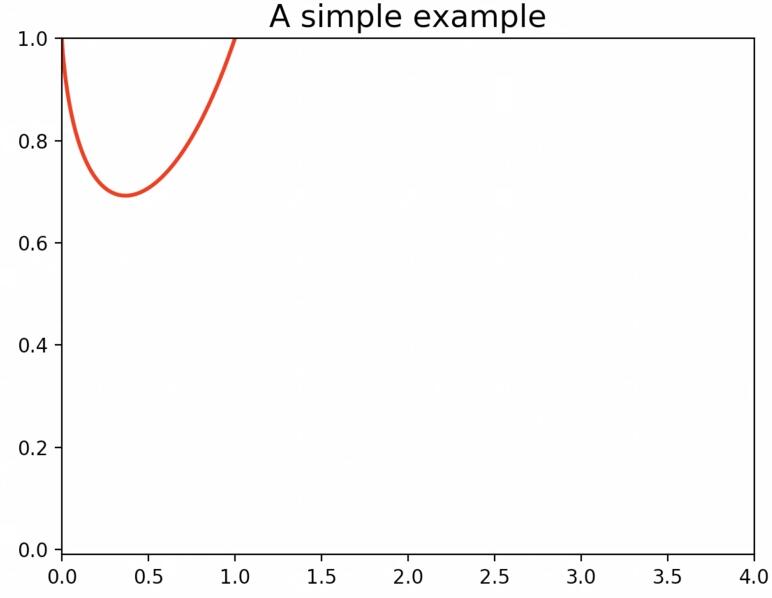
导数

数学知识中我们知道导数dy（也就是沿着函数方向的切线）能够知道函数值的趋势，也就是梯度，导数范围是[-1,1], 增加或者是减少；如图所示：
假设我们X0初始值是1，X1需要往0的方向去求取最小值，在x为1的时候导数为负数。
假设我们X0初始值是0，X1需要往1的方向去求最小值，在x为0时导数为正数。

学习率

假如我们设定在求最小值过程中，每次x的变化是0.05，直到找到最小值，这个0.05在机器学习中称为步长，也叫学习率lr（learning-rate）。

由于导数影响函数趋势方向，dy*lr能给表示x的变化方向，当导数为1表示非常陡峭，可以加快步速，当导数趋近0时需要放慢步速，表示将要到达极值。

求导过程

根据学习率，我们得出 X1 = X0 - dy * lr，其中lr这里设置为0.05，dy即对函数求导：

// 求导过程
y = x^x
// 对函数降幂
lny = xlnx
// 左右两边分别求导
1/y * dy = 1 + lnx
// 左右两边同时乘以y
dy = (1+ lnx)y
// 因为y = x^x
dy = (1+lnx) * x^x

得出dy = (1+lnx) * x^x

js的实现

// 函数
const y = function(x) {
   return Math.pow(x, x);
};
// 导数
const dy = function(x) {
    return (Math.log(x) + 1) * x * x;
};
// 步长
const step = 0.05;
// 训练次数
const tranTimes = 1000
// 初始值x
let start = 1;

for (let count = 1; count < tranTimes; count++) {
  start = start - dy(start) * step;
  console.log(start, y(start));
}

输出结果：

0.95 0.9524395584709955
index.html:21 0.9071896099092381 0.9154278618565974
index.html:21 0.8700480926733879 0.8859306522286503
index.html:21 0.8374677719259425 0.8619622953920216
index.html:21 0.8086201886475226 0.8421712374320481
index.html:21 0.7828717701107167 0.8256070591665992
index.html:21 0.7597286934875257 0.8115828484109726
index.html:21 0.7387996916491102 0.7995903987023993
index.html:21 0.719770279950795 0.789246056834791
index.html:21 0.7023844759968008 0.7802550613870627
index.html:21 0.6864315663021606 0.7723874207927244
index.html:21 0.6717363517465544 0.7654612085706618
index.html:21 0.6581518405386136 0.7593307516282222
index.html:21 0.6455536948955527 0.7538781218982149
index.html:21 0.6338359551226174 0.7490069045677286
index.html:21 0.6229077080606727 0.7446375646724406
index.html:21 0.612690463173548 0.7407039548649291
index.html:21 0.6031160654545613 0.7371506504493626
index.html:21 0.5941250201862136 0.7339308925190816
index.html:21 0.5856651369738545 0.7310049838252315
index.html:21 0.5776904236672961 0.7283390256729259
index.html:21 0.570160177606762 0.7259039144927062
index.html:21 0.5630382339758626 0.7236745381284763
//省略
index.html:21 0.3678794436566963 0.6922006275553464
index.html:21 0.36787944361098257 0.6922006275553464
index.html:21 0.36787944356610974 0.6922006275553464
index.html:21 0.3678794435220623 0.6922006275553464
index.html:21 0.36787944347882506 0.6922006275553464
index.html:21 0.3678794434363831 0.6922006275553464
index.html:21 0.3678794433947219 0.6922006275553464
index.html:21 0.36787944335382694 0.6922006275553464
index.html:21 0.3678794433136842 0.6922006275553464
index.html:21 0.3678794432742799 0.6922006275553464
index.html:21 0.36787944323560035 0.6922006275553464
index.html:21 0.36787944319763227 0.6922006275553464
index.html:21 0.3678794431603626 0.6922006275553464
index.html:21 0.36787944312377846 0.6922006275553464
index.html:21 0.36787944308786724 0.6922006275553464
index.html:21 0.36787944305261655 0.6922006275553464
index.html:21 0.3678794430180143 0.6922006275553464
index.html:21 0.3678794429840485 0.6922006275553464
index.html:21 0.36787944295070746 0.6922006275553464
index.html:21 0.3678794429179797 0.6922006275553464
index.html:21 0.36787944288585395 0.6922006275553464
index.html:21 0.3678794428543191 0.6922006275553464
index.html:21 0.3678794428233643 0.6922006275553464
index.html:21 0.3678794427929789 0.6922006275553464
index.html:21 0.36787944276315243 0.6922006275553464
index.html:21 0.3678794427338746 0.6922006275553464
index.html:21 0.36787944270513523 0.6922006275553464
index.html:21 0.3678794426769245 0.6922006275553464
index.html:21 0.3678794426492327 0.6922006275553464
index.html:21 0.3678794426220503 0.6922006275553464
index.html:21 0.36787944259536787 0.6922006275553464

通过结果可以判断出，当x约等于0.367879442时，y有最小值0.6922006275553464

在学习率为0.05的情况下，1000次训练中，在最后约100次震荡中，输出的的y结果都是一样的，也就是说我们的训练次数是过多的，可以适当调整；

但如果我们一开始的设置的学习率是0.01，1000次训练，最后一次输出，【0.3721054412801767 0.6922173655754094】,得出不是极值，这时候也需要适当的调整，这叫做调参，得出最适合的训练模型。

全局最小值

至此，y = x^x求最小值已经完成，但是实际机器学习的函数并没有那么简单，也就是下面这种图。

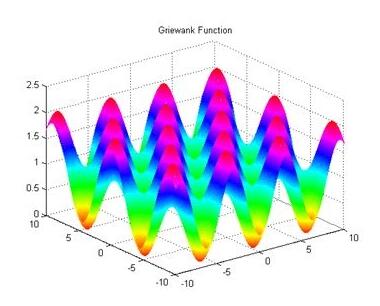
简化一下函数图像，如下图，上面的求值方式可能只求到第一个最低点，称为局部最低点，实际上我们要求的是全局最低点在第二个最低点。

所以我们继续调参：

dy(start) * step完全依赖上一步的趋势，导致震荡不到全局最低点。所以我们可以添加一些系数，设置当前导数影响系数为0.9，上一导数影响系数为0.1，0.9 * dy(start) * step + 0.1 * dy(lastStart) * step，可以保留一些梯度直到全局最低点。

当然这里的系数和参数，都是假定的，都需要实际尝试去得到最适合的数，所以听说算法工程师也会自嘲调参工程师。

来自：https://segmentfault.com/a/1190000020030764

链接: https://fly63.com/article/detial/4609