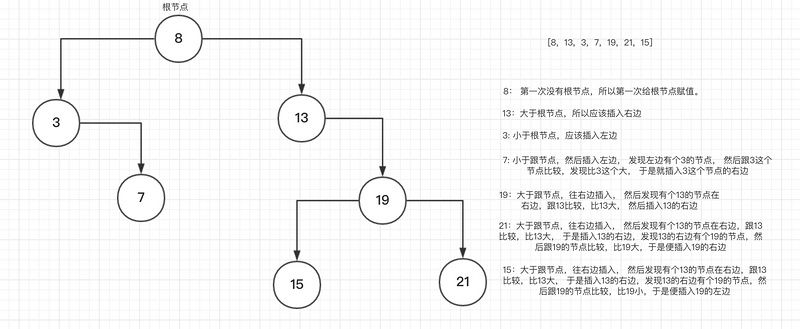
2. 二叉树的遍历

/* 
  前序遍历：根节点->左子树->右子树
  中序遍历：左子树->根节点->右子树
  后序遍历：左子树->右子树->根节点
*/

前序遍历

//前序遍历
    this.preorderTraversal = function (callback) {
        if (this.root === null) {   //传入根节点
            console.warn('请先初始化二叉排序树');
            return;
        }
        var fn = function (node, callback) {
            if (node !== null) {  //当前节点不等于空的时候,先遍历自身节点, 再遍历左子树节点, 最后遍历右子树节点
               callback(node); //自身
               fn(node.left, callback); //左子树
               fn(node.right, callback) //右子树
            }
        }
        fn(this.root, callback)
    }

中序遍历

//中序遍历
    this.orderTraversal = function (callback) { //从小到大
        callback = callback || function () {};
        if (this.root === null) {  //传入根节点
            console.warn('请先初始化二叉排序树');
            return;
        }
        var fn = function (node, callback) {
            if (node !== null) { //当前节点不等于空的时候,先遍历左子树节点, 再遍历自身节点, 最后遍历右子树节点
               fn(node.left, callback);  //左子树
               callback(node); //自身
               fn(node.right, callback);  //右子树 
            }
        }
        fn(this.root, callback)
    }

后序遍历

//后序遍历
    this.postorderTraversal = function (callback) {
        if (this.root === null) {  //传入根节点
            console.warn('Please initialize first');
            return;
        }
        var fn = function (node, callback) {
            if (node !== null) {  //当前节点不等于空的时候,先遍历左子树节点, 再遍历右子树节点, 最后遍历自身节点
               fn(node.left, callback); //左子树
               fn(node.right, callback);  //右子树
               callback(node);  //自身
            }
        }
        fn(this.root, callback)
    }

3.查找最小值

   this.min = function () {  //查找最小值就一直往左边查找就行了,直到左边没有节点为止,那就证明已经到最小值了
       var fn = function (node) {
           if (node == null) {  //传入根节点
               console.warn('请先初始化二叉排序树');
               return null;
           }
           if (node.left) { //查找当前左子树有没有节点, 有点话继续递归查找该左节点存不存在左节点
               return fn(node.left);
           }else{ //直到当前节点不在存在左节点,证明取到最小值了
               return node;
           }
       }
       return fn(this.root)   
   }

4.查找最大值

   //查找最大值
   this.max = function () {  //跟查找最小值一样,  查找最大值就一直往右边查找就行了
       var fn = function (node) {
           if (node == null) {  //传入根节点
               console.warn('请先初始化二叉排序树');
               return null;
           }
           if (node.right) { 
               return fn(node.right);
           }else{
               return node;
           }
       }
       return fn(this.root) 
   }

5.删除节点

//删除节点
    this.remove = function (key) {
        var fn = function (node, key) {
            if (node === null) {  //传入初始节点
                console.warn('请先初始化二叉排序树');
                return null;
            }
            if (node.key > key) { //初始节点的值大于我要删除节点的值, 说明我要删除的节点在初始节点的左边
                node.left = fn(node.left, key) //递归一直寻找左边的子节点,直到找到null 为止
                return node;
            }else if (node.key < key) {//初始节点的值小于我要删除节点的值, 说明我要删除的节点在初始节点的右边
                node.right = fn(node.right, key);
                return node;
            }else { //当前节点的值等于我要删除节点的值,说明找到要删除的节点了

                //当前节点的左右两边分支都为空时,直接把当前节点置为null,返回出去
                if (node.left === null && node.right === null) { 
                    node = null;
                    return node;
                }

                //当前节点只有左边为空时, 直接引入右边的分支替换成当前分支
                if (node.left === null) { 
                    node = node.right;
                    return node;
                }

                //当前节点只有右边为空时, 直接引入左边的分支替换成当前分支
                if (node.right == null) {  
                    node = node.left;
                    return node;
                }

                //当左右两边节点都不为空时, 就需要找一个值来替换当前的值, 为了结构的完整性,最好是大于左边的值,
                //而且小于右边的, 这个值的最佳选择就是当前节点右边的最小值, 这样就能比左边的大,  比右边的小

                //去右边寻找最小值, 而且最小值应该在左子树上
                var minNode = rightMinNode(node.right);

                // 那我们就要删除右边最小值的那个分支, 然后把值赋值到当前节点上

                fn(node, minNode.key) //执行右边最小值删除操作

                node.key = minNode.key
                return node;
            }
        }
        var rightMinNode = function (node) {
            if (node.left === null) { //如果第一个右子树的左子树上为空的话, 那他就是最小值, 如果存在那就往左子树上在进行查询,知道左子树为null时, 那就是最小值
                return node;
            }
            return rightMinNode(node.left)
        }
        fn(this.root, key)
    }